1. Background

The softmax function is a fundamental operation in deep learning that converts vectors of real numbers into probability distributions. This blog post explores the softmax function's implementation and optimization using Triton, a programming framework for efficient GPU computations.

The softmax function transforms an input vector into a probability distribution where all elements sum to 1.

1.1. softmax - vector form

$${𝒐}_{𝑖}=\text{softmax}\left({𝒙}_{𝑖}\right)=\frac{{𝑒}^{{𝒙}_{𝑖}}}{\sum _{𝑗=1}^{𝑑}{𝑒}^{{𝒙}_{𝑗}}}$$

where:

• $𝒙\in {\mathrm{ℝ}}^{𝑑}$: input vector.
• $𝒐\in {\mathrm{ℝ}}^{𝑑}$: output vector, probability distribution.

2. Gradient of softmax (vector form)

We will compute gradients $\frac{\partial 𝐿}{\partial 𝒙}$ given $\frac{\partial 𝐿}{\partial 𝒐}$, where $𝐿$ is loss function, $𝒐$ is softmax output.

2.1. Jacobian matrix

softmax is a vector function, the Jacobian matrix is the matrix of all partial derivatives:

$$\frac{\partial 𝒐}{\partial 𝒙}=𝑱=\left(\begin{array}{cccc}\frac{\partial {𝒐}_1}{\partial {𝒙}_1}& \frac{\partial {𝒐}_1}{\partial {𝒙}_2}& \dots & \frac{\partial {𝒐}_1}{\partial {𝒙}_{𝑑}}\\ \frac{\partial {𝒐}_2}{\partial {𝒙}_1}& \frac{\partial {𝒐}_2}{\partial {𝒙}_2}& \dots & \frac{\partial {𝒐}_2}{\partial {𝒙}_{𝑑}}\\ \text{ ⋮}& \text{ ⋮}& \text{ ⋱}& \text{ ⋮}\\ \frac{\partial {𝒐}_{𝑑}}{\partial {𝒙}_1}& \frac{\partial {𝒐}_{𝑑}}{\partial {𝒙}_2}& \dots & \frac{\partial {𝒐}_{𝑑}}{\partial {𝒙}_{𝑑}}\end{array}\right)$$

For softmax, the derivative has two cases:

1. when $𝑖=𝑗$, consider ${𝒐}_{𝑖}=\frac{{𝑒}^{{𝒙}_{𝑖}}}{{\sum }_{𝑗=1}^{𝑑}{𝑒}^{{𝒙}_{𝑗}}}$, the derivative is:

   $$\frac{\partial {𝒐}_{𝑖}}{\partial {𝒙}_{𝑖}}={𝒐}_{𝑖}\left(1-{𝒐}_{𝑖}\right)$$

2. similarly, when $𝑖\ne 𝑗$:

   $$\frac{\partial {𝒐}_{𝑖}}{\partial {𝒙}_{𝑗}}=-{𝒐}_{𝑖}{𝒐}_{𝑗}$$

Thus, $\left(𝑖,𝑗\right)$-th element in Jacobian matrix will be:

$${𝑱}_{𝑖𝑗}={𝒐}_{𝑖}\left({𝛿}_{𝑖𝑗}-{𝒐}_{𝑗}\right)$$

where $𝑱$ has shape $\left[𝑑\times 𝑑\right]$ and ${𝛿}_{𝑖𝑗}$ is the Kronecker delta, which is 1 if $𝑖=𝑗$ and 0 otherwise.

In matrix form, the Jacobian of the softmax is:

$$𝑱=\text{diag}\left(𝒐\right)-𝒐{𝒐}^{𝑇}$$

where:

• $𝒐$ is the output of softmax, the shape is $\left[𝑑\right]$.
• $\text{diag}\left(𝒐\right)$ is a diagonal matrix of $𝒐$, the shape is $\left[𝑑\times 𝑑\right]$.
• $𝒐{𝒐}^{𝑇}$ is the outer product of $𝒐$ with itself, the shape is $\left[𝑑\times 𝑑\right]$.

2.2. gradient of $\frac{\partial 𝐿}{\partial 𝒙}$

Given $\frac{\partial 𝐿}{\partial 𝒐}$, we can compute $\frac{\partial 𝐿}{\partial 𝒙}$ using the Jacobian matrix:

$$\frac{\partial 𝐿}{\partial 𝒙}=\frac{\partial 𝒐}{\partial 𝒙}\cdot \frac{\partial 𝐿}{\partial 𝒐}={𝑱}^{𝑇}\cdot \frac{\partial 𝐿}{\partial 𝒐}$$

where $\frac{\partial 𝐿}{\partial 𝒐}$ has shape $\left[𝑑\right]$, ${𝑱}^{𝑇}$ has shape $\left[𝑑\times 𝑑\right]$, and $\frac{\partial 𝐿}{\partial 𝒙}$ has shape $\left[𝑑\right]$.

2.3. avoid explicit Jacobian

For the $𝑖$-th element of $\frac{\partial 𝐿}{\partial 𝒙}$, we can decompose the computation to:

$$\frac{\partial 𝐿}{\partial {𝒙}_{𝑖}}={𝒐}_{𝑖}\left(\frac{\partial 𝐿}{\partial {𝒐}_{𝑖}}-\sum _{𝑗=1}^{𝑑}{𝒐}_{𝑗}\frac{\partial 𝐿}{\partial {𝒐}_{𝑗}}\right)$$

This leads to an efficient vector form:

$${𝑠}_{\text{grad}}={\left(𝒐\ast \frac{\partial 𝐿}{\partial 𝒐}\right)}_{\text{sum}}$$$$\frac{\partial 𝐿}{\partial 𝒙}=𝒐\ast \left(\frac{\partial 𝐿}{\partial 𝒐}-{𝑠}_{\text{grad}}\right)$$

3. softmax - batch form

$𝑿$: A batch of input vectors.

$$𝑿\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$$

where:

• $𝑁$ is batch size.
• $𝑑$ is vector dimension.

3.1. forward pass

$$𝑬={𝑒}^{𝑿}$$$$𝒔=\sum _{𝑗=1}^{𝑑}{𝑒}^{{𝑿}_{𝑖𝑗}}$$$$𝑶=\frac{𝑬}{𝒔}$$

where $𝑬\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$, $𝒔\in {\mathrm{ℝ}}^{𝑁\times 1}$, $𝑶\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$.

3.2. backward pass

We have gradient with respect to softmax output:

$$\frac{\partial 𝐿}{\partial 𝑶}\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$$

we compute the gradient:

$${𝒔}_{\text{grad }}={\left(𝑶\ast \frac{\partial 𝐿}{\partial 𝑶}\right)}_{\text{ row\_sum }}\in {\mathrm{ℝ}}^{𝑁\times 1}$$

where $𝑶$ has size $\left[𝑁\times 𝑑\right]$, and $\frac{\partial 𝐿}{\partial 𝑶}$ has size $\left[𝑁\times 𝑑\right]$.

$$\frac{\partial 𝐿}{\partial 𝑿}=𝑶\ast \left(\frac{\partial 𝐿}{\partial 𝑶}-{𝒔}_{\text{ grad}}\right)$$

where $\frac{\partial 𝐿}{\partial 𝑿}\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$ and $𝑶\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$ and ${𝒔}_{\text{grad }}\in {\mathrm{ℝ}}^{𝑁\times 1}$ will be broadcasted to ${\mathrm{ℝ}}^{𝑁\times 𝑑}$.

4. Implementation

In practice, we subtract the maximum value from each row before applying exp() to prevent numerical overflow:

4.1. real forward pass

For input $𝑿\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$:

$${𝑿}_{\text{max }}=\max \left(𝑿\right)\in {\mathrm{ℝ}}^{𝑁\times 1}$$$$𝑬={𝑒}^{𝑿-{𝑿}_{\text{ max}}}$$$$𝒔=\sum _{𝑗=1}^{𝑑}{𝑒}^{{𝑿}_{𝑖𝑗}-{𝑿}_{\text{ max}}}$$$$𝑶=\frac{𝑬}{𝒔}$$

4.2. real backward pass

we have $\frac{\partial 𝐿}{\partial 𝑶}\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$ and cached $𝑶\in {\mathrm{ℝ}}^{𝑁\times 𝑑}$

$${𝒔}_{\text{grad }}={\left(𝑶\ast \frac{\partial 𝐿}{\partial 𝑶}\right)}_{\text{ row\_sum}}$$$$\frac{\partial 𝐿}{\partial 𝑿}=𝑶\ast \left(\frac{\partial 𝐿}{\partial 𝑶}-{𝒔}_{\text{ grad}}\right)$$

4.3. a real example

give a real example to show how to implement softmax and its backward pass in pytorch and triton.

forwards pass is as follows:

$$𝑋=\left(\begin{array}{ccc}1.0& 2.0& 3.0\\ 1.0& 3.0& 5.0\end{array}\right)$$$${𝑋}_{\text{max }}=\left(\begin{array}{c}3.0\\ 5.0\end{array}\right)$$$$𝑋-{𝑋}_{\text{ max }}=\left(\begin{array}{ccc}-2.0& -1.0& 0.0\\ -4.0& -2.0& 0.0\end{array}\right)$$$$𝐸={𝑒}^{𝑋-{𝑋}_{\text{ max}}}=\left(\begin{array}{ccc}{𝑒}^{-2.0}& {𝑒}^{-1.0}& {𝑒}^{0.0}\\ {𝑒}^{-4.0}& {𝑒}^{-2.0}& {𝑒}^{0.0}\end{array}\right)$$$$𝐸=\left(\begin{array}{ccc}0.1353& 0.3679& 1.0000\\ 0.0183& 0.1353& 1.0000\end{array}\right)$$$$𝑆=\left(\begin{array}{c}1.5032\\ 1.1536\end{array}\right)$$$$𝑂=\frac{𝐸}{𝑆}=\left(\begin{array}{ccc}0.0900& 0.2447& 0.6652\\ 0.0159& 0.1173& 0.8668\end{array}\right)$$

backward pass is as follows:

$$𝑑𝑂=\left(\begin{array}{ccc}0.1& 0.2& 0.7\\ 0.2& 0.3& 0.5\end{array}\right)$$$${𝑠}_{\text{grad }}=\left(\begin{array}{c}0.2036\\ 0.2597\end{array}\right)$$$$𝑑𝑋=𝑂\ast \left(𝑑𝑂-{𝑠}_{\text{ grad}}\right)$$$$𝑑𝑋=\left(\begin{array}{ccc}-0.0381& -0.0792& 0.1173\\ -0.0043& -0.0202& 0.0245\end{array}\right)$$

4.4. native pytorch implementation

import torch
import torch.nn.functional as F

# Custom Forward Pass (Numerically Stable Softmax)
def softmax_forward(X):
    X_max = torch.max(X, dim=1, keepdim=True)[0]  # Shape: (N, 1)
    E = torch.exp(X - X_max)                     # Shape: (N, d)
    S = torch.sum(E, dim=1, keepdim=True)        # Shape: (N, 1)
    O = E / S                                    # Shape: (N, d)
    return O

# Custom Backward Pass (Gradient Calculation)
def softmax_backward(dL_dO, O):
    s_grad = torch.sum(O * dL_dO, dim=1, keepdim=True)  # Shape: (N, 1)
    dL_dX = O * (dL_dO - s_grad)                        # Shape: (N, d)
    return dL_dX

# Example Inputs
X = torch.tensor([[1.0, 2.0, 3.0], [1.0, 3.0, 5.0]], requires_grad=True)
dL_dO = torch.tensor([[0.1, 0.2, 0.7], [0.2, 0.3, 0.5]])

# Custom Implementation - Forward
O_custom = softmax_forward(X)

# PyTorch Implementation - Forward
O_pytorch = F.softmax(X, dim=1)

# Verify Forward Output
print("Custom Softmax Output:\n", O_custom)
print("PyTorch Softmax Output:\n", O_pytorch)
print("Forward Pass Match:", torch.allclose(O_custom, O_pytorch))

# Custom Implementation - Backward
dL_dX_custom = softmax_backward(dL_dO, O_custom)

# PyTorch Automatic Gradient Calculation
O_pytorch.backward(dL_dO)  # Computes gradient using PyTorch autograd
dL_dX_pytorch = X.grad

# Verify Backward Output
print("\nCustom Gradient w.r.t Input:\n", dL_dX_custom)
print("PyTorch Gradient w.r.t Input:\n", dL_dX_pytorch)
print("Backward Pass Match:", torch.allclose(dL_dX_custom, dL_dX_pytorch))

output:

Custom Softmax Output:
 tensor([[0.0900, 0.2447, 0.6652],
        [0.0159, 0.1173, 0.8668]], grad_fn=<DivBackward0>)
PyTorch Softmax Output:
 tensor([[0.0900, 0.2447, 0.6652],
        [0.0159, 0.1173, 0.8668]], grad_fn=<SoftmaxBackward0>)
Forward Pass Match: True

Custom Gradient w.r.t Input:
 tensor([[-0.0381, -0.0792,  0.1173],
        [-0.0043, -0.0202,  0.0245]], grad_fn=<MulBackward0>)
PyTorch Gradient w.r.t Input:
 tensor([[-0.0381, -0.0792,  0.1173],
        [-0.0043, -0.0202,  0.0245]])
Backward Pass Match: True

4.5. triton implementation

from typing import Optional

import torch
import triton
import triton.language as tl


@triton.jit
def softmax_fwd_kernel(
    X,
    O,
    D: tl.constexpr,
    B: tl.constexpr
):
    i_n = tl.program_id(0)
    o_d = tl.arange(0, B)
    m_d = o_d < D

    X_max = tl.max(tl.load(X + i_n * D + o_d, mask=m_d, other=-float('inf')), 0)
    E = tl.exp(tl.load(X + i_n * D + o_d, mask=m_d, other=-float('inf')) - X_max)
    S = tl.sum(E, 0)
    P = E / S

    tl.store(O + i_n * D + o_d, P.to(O.dtype.element_ty), mask=m_d)


@triton.jit
def softmax_bwd_kernel(
    O,
    dO,
    dX,
    D: tl.constexpr,
    B: tl.constexpr
):
    i_n = tl.program_id(0)
    o_d = tl.arange(0, B)
    m_d = o_d < D

    P = tl.load(O + i_n * D + o_d, mask=m_d, other=0.)
    dP = tl.load(dO + i_n * D + o_d, mask=m_d, other=0.)
    s_grad = tl.sum(P * dP, 0)
    dX_row = P * (dP - s_grad)

    tl.store(dX + i_n * D + o_d, dX_row.to(dX.dtype.element_ty), mask=m_d)


def softmax_fwd(
    X: torch.Tensor,
    dtype: Optional[torch.dtype] = torch.float
) -> torch.Tensor:
    shape = X.shape
    X = X.view(-1, X.shape[-1])

    N, D = X.shape
    B = triton.next_power_of_2(D)

    O = torch.empty_like(X, dtype=dtype)
    softmax_fwd_kernel[(N,)](
        X=X,
        O=O,
        D=D,
        B=B
    )
    return O.view(*shape)


def softmax_bwd(
    O: torch.Tensor,
    dO: torch.Tensor,
    dtype: Optional[torch.dtype] = torch.float
) -> torch.Tensor:
    shape = O.shape
    O = O.view(-1, O.shape[-1])
    dX = torch.empty_like(O, dtype=dtype)

    N, D = O.shape
    B = triton.next_power_of_2(D)
    softmax_bwd_kernel[(N,)](
        O=O,
        dO=dO,
        dX=dX,
        D=D,
        B=B
    )
    return dX.view(*shape)

# Test code to verify correctness
import torch.nn.functional as F

# Example inputs
X = torch.tensor([[1.0, 2.0, 3.0], [1.0, 3.0, 5.0]], requires_grad=True, device='cuda')
dP = torch.tensor([[0.1, 0.2, 0.7], [0.2, 0.3, 0.5]], device='cuda')

# Forward pass
P_triton = softmax_fwd(X)
P_torch = F.softmax(X, dim=1)

# Verify forward pass
print( "P_triton:\n", P_triton)
print( "P_torch:\n", P_torch)
print("Forward Pass Match:", torch.allclose(P_triton, P_torch))

# Backward pass

dX_triton = softmax_bwd(P_triton, dP)
P_torch.backward(dP)
dX_torch = X.grad

# Verify backward pass
print( "dX_triton:\n", dX_triton)
print( "dX_torch:\n", dX_torch)
print("Backward Pass Match:", torch.allclose(dX_triton, dX_torch))

output:

P_triton:
 tensor([[0.0900, 0.2447, 0.6652],
        [0.0159, 0.1173, 0.8668]], device='cuda:0')
P_torch:
 tensor([[0.0900, 0.2447, 0.6652],
        [0.0159, 0.1173, 0.8668]], device='cuda:0', grad_fn=<SoftmaxBackward0>)
Forward Pass Match: True
dX_triton:
 tensor([[-0.0381, -0.0792,  0.1173],
        [-0.0043, -0.0202,  0.0245]], device='cuda:0')
dX_torch:
 tensor([[-0.0381, -0.0792,  0.1173],
        [-0.0043, -0.0202,  0.0245]], device='cuda:0')
Backward Pass Match: True

5. Results: speed comparison

The performance comparison between PyTorch and Triton implementations reveals:

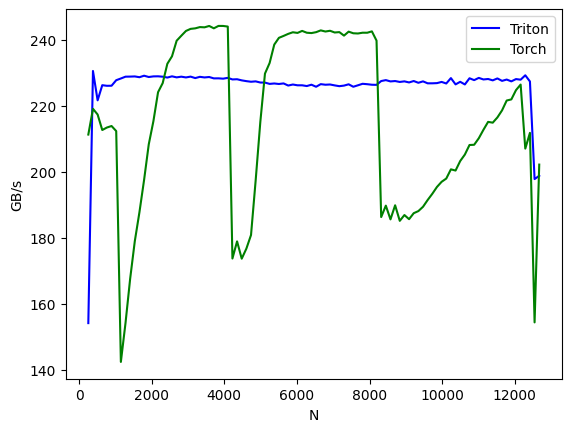
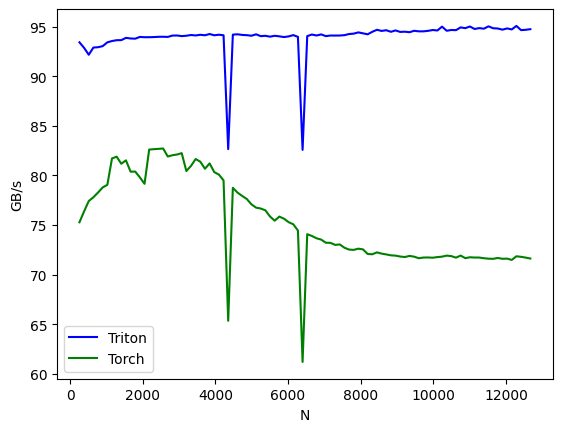
Results show

• forward pass: triton implementation is stable, while the PyTorch implementation is faster for most batch sizes but shows fluctuations for a few.
• backward pass: triton implementation outperforms the pytorch implementation across most batch sizes. (the comparison may not be entirely fair, as triton caches the output $𝑂$, whereas pytorch's handling intermediate values is unclear.)

6. Notations

symbol	shape	definition
$𝒙$	$𝑑$	Input vector
$𝒐$	$𝑑$	Output vector (probability distribution)
$𝐿$	Scalar	Loss function
$𝑱$	$𝑑\times 𝑑$	Jacobian matrix
$𝑿$	$𝑁\times 𝑑$	Batch of input vectors (matrix)
$𝑶$	$𝑁\times 𝑑$	Batch output probabilities
$\frac{\partial 𝐿}{\partial 𝑶}$	$𝑁\times 𝑑$	Gradient w.r.t. output probabilities
$\frac{\partial 𝐿}{\partial 𝑿}$	$𝑁\times 𝑑$	Gradient w.r.t. input vectors
${𝑠}_{\text{grad}}$	$𝑁\times 1$	Summation of gradients, ${𝑠}_{\text{grad }}={\left(𝑶\ast \frac{\partial 𝐿}{\partial 𝑶}\right)}_{\text{ sum}}$

Note:

• Symbols like $𝑥$, $𝒙$, $𝑿$ represent scalars, vectors, or matrices, where uppercase denotes batch forms.
• ${𝑿}_{:,𝑖}$ denotes a column vector, ${𝑿}_{𝑖,:}$ denotes a row vector, ${𝑿}_{𝑖,𝑗}$ and denote the $\left(𝑖,𝑗\right)$-th element
• ${𝒙}_{𝑖}$ denote the $𝑖$-th element.